Improving compaction in Cassandra with cardinality estimation

Wasteful Bloom filter allocation

Compaction is the process whereby Cassandra merges its log-structured data files to evict obsolete or deleted rows. These data files (sstables) are composed of several components to make reads efficient.

The first component that gets consulted on a read is the Bloom filter. A Bloom filter is a probabilistic set that takes just a few bits per key stored, and is thus much more memory-efficient than actually storing the partition keys themselves. The bloom filter takes 1-2GB of memory per billion partitions. (By default, Cassandra uses a smaller bloom filter for Leveled compaction since the leveling means we expect to consult the bloom filter less often for sstables that don't contain the partition in question.)

Our first big concern was moving this memory off-heap to support larger data sets. With that done, we're looking at other ways to improve this.

One big gain would be avoiding unnecessary worst-case bloom filter allocations. That is, given two initial sstables, the result of the compaction could be this for two sstables that don't overlap at all:

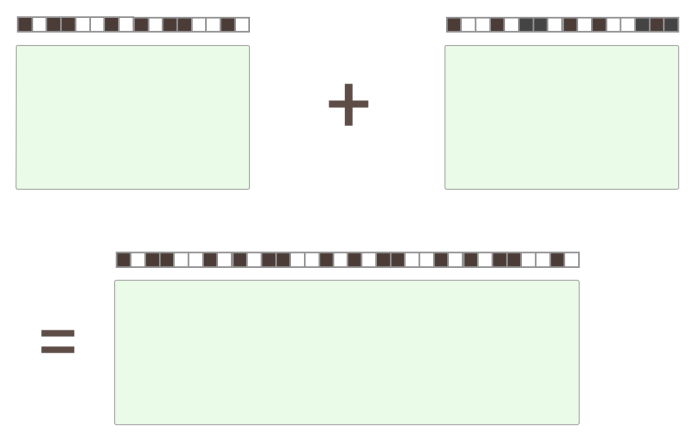
or, it could be this if they overlap entirely:

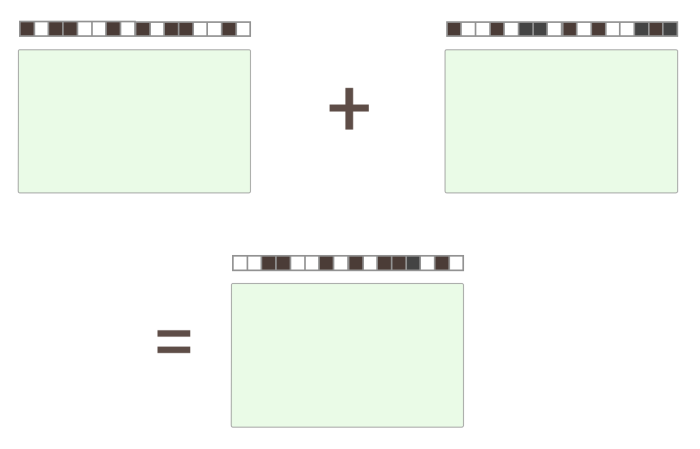
Or, it could be anywhere in between.

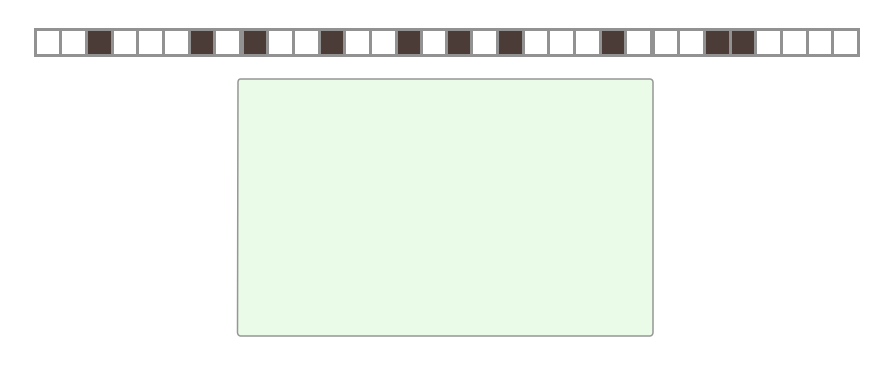
Because bloom filters are not re-sizeable, we need to pre-allocate them at the start of the compaction, but at the start of the compaction, we don't know how much the sstables being compacted overlap. Since bloom filter performance deteriorates dramatically when over-filled, we allocate our bloom filters to be large enough even if the sstables do not overlap at all. Which means that if they do overlap (which they should if compaction is doing a good job picking candidates), then we waste space -- up to 100% per sstable compacted:

Accurate estimates with HyperLogLog

To solve this problem, we need a fairly accurate estimate of how much the compacting sstables overlap, before we start merging them. This is a good fit for a class of algorithms called cardinality estimation. For instance, given a set of evenly distributed random numbers, we can estimate how many are unique by tracking the smallest number in the set:

If the maximum possible value is m, and the smallest value we find is x, we can then estimate there to be about m/x unique values in the total set. For instance, if we scan a dataset of numbers between 0 and 1, and find that the smallest value in the set is 0.01, it's reasonable to assume there are roughly 100 unique values in the set; any more and we would expect to see a smaller minimum value.

The actual algorithm used in Cassandra 2.1 is called HyperLogLog, as implemented in Java by AddThis. (Technically, this implements a variant called HyperLogLog++.) The details are out of scope for this post, but I can highly recommend Damn Cool Algorithms' explanation.

Crucially, and unlike the simplistic min-tracking example, HyperLogLog lets us combine two cardinality estimates to get an estimate of the union of the sets they summarize, which is exactly what we need for estimating how many elements will be in the merged bloom filter. Experimental results show that we save about 40% of the bloom filter overhead by getting this more accurate count, although this will be highly workload-dependent.

Future work

Potentially even more useful would be using cardinality estimation to pick better compaction candidates. Instead of blindly merging sstables of a similar size a la SizeTieredCompactionStrategy:

we could merge the candidates that overlap most, which would be a big improvement both for overwrite-heavy and append-mostly workloads:

Unfortunately, the HyperLogLog estimates we use for bloom filter estimates are large enough (~10KB per sstable) that keeping them on-heap permanently would lose a lot of our recent gains, and keeping them off-heap would require re-engineering stream-lib. While that isn't a deal breaker, we may be able to do better by using minhash to approximate the Jaccard similarity coefficient rather than estimating merged cardinality directly with HyperLogLog. Follow CASSANDRA-6474 for the gory details, but you can expect to see similarity-based compaction in Cassandra later this year.