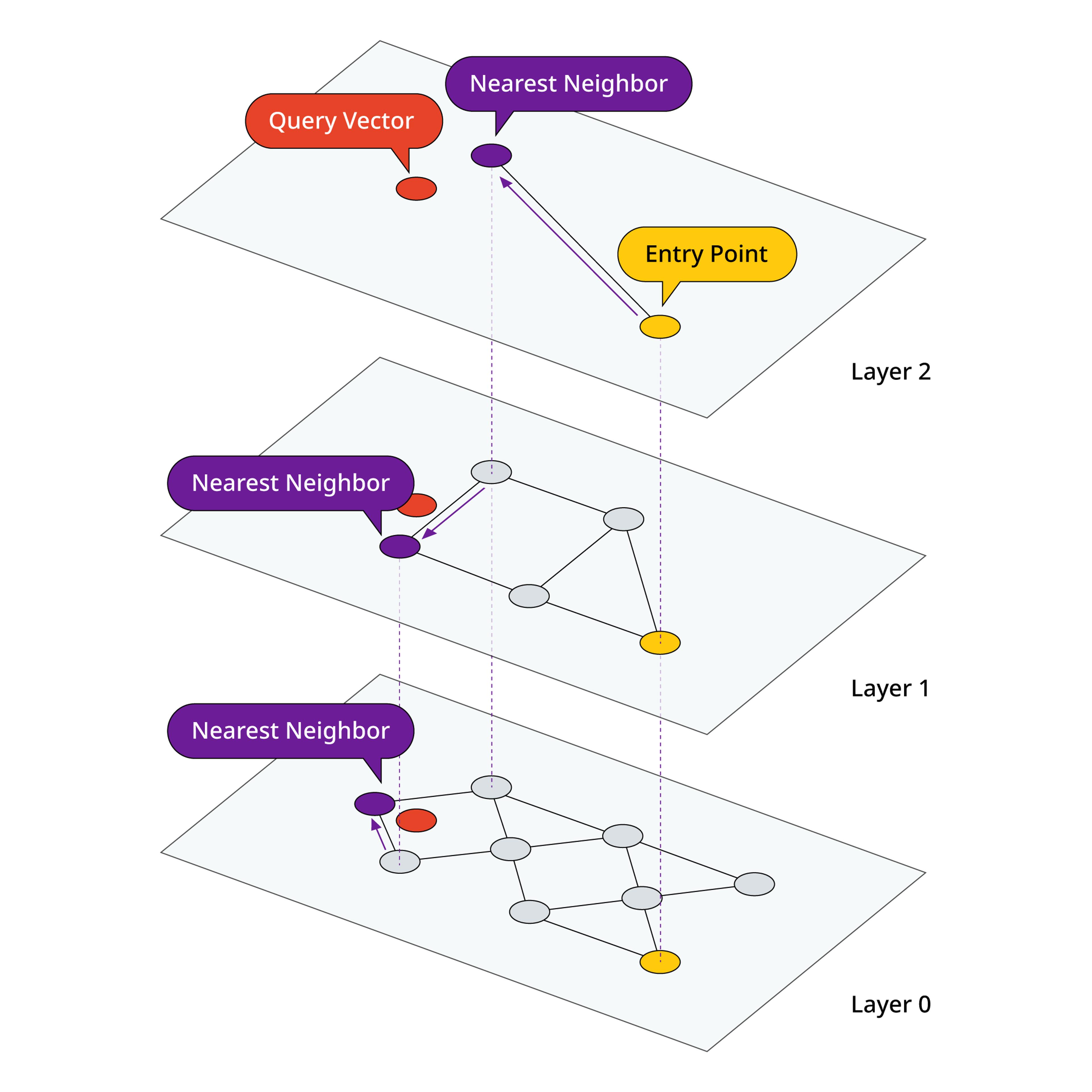
What Types of Things Can Be Embedded?
One of the key opportunities that vector embeddings can provide is the ability to represent any type of data as a vector embedding. There are many current examples where text and image embeddings are being heavily used to create solutions like natural language processing (NLP) Chatbots using tools like GPT-4 or generative image processors like Dall-E 2.
Text Embeddings
Text embeddings are probably the easiest ones to understand and we have been using text embeddings as the foundation for most of our examples. Text embeddings start as a data corpus of text-based objects so for large language models like Word2Vec they use large datasets from things like Wikipedia. But text embeddings can be used for pretty much any type of text-based dataset that you want to quickly and easily search for nearest neighbor or semantically similar results.
For example, say you want to create an NLP chatbot to answer questions about your product, you can use text embeddings of the product documentation and product FAQs that can allow for the chatbot to respond to queries based on questions posed. Or what about feeding all of the cookbooks you have collected over the years as the data corpus and using that data to provide recipes based on all the ingredients you have in your pantry? What text embeddings bring is the ability to take unstructured data like words, paragraphs and documents and represent them in a structured form.
Image Embeddings
Image embeddings like text embeddings can represent multiple different aspects of images. From full images down to individual pixels, image embeddings provide the ability to classify the set of features an image has, and present those features mathematically for analysis by machine learning models or for use by image generators like Dall-E 2.
Probably one of the most common usages of image embeddings is used for classification and reverse image search. Say for example I have a picture of a snake that was taken in my backyard and I would like to know what type of snake it is and if it is venomous. With a large data corpus of all the different types of snakes, I can feed the image of my snake into the vector database of all the vector embeddings of snakes and find the closest neighbor to my image. From that semantic search I can pull all the “attributes” of the closest nearest neighbor image to my snake and determine what kind of snake it is and if I should be concerned.
Another example of how vector embeddings can be used is automated image editing like Google Magic Photo Editor which allows for images to be edited by generative AI making edits to specific parts of an image like removing people from the background or adding better composition.
Product Embeddings
Another example of how vector embeddings can be used is in recommendation engines. Product embeddings can be anything from movies and songs to shampoos. With product embeddings e-commerce sites can observe shoppers' behaviors through search results, click stream and purchase patterns and make recommendations based on semantic similarly, recommendations for new or niche products. Say for example that I visit my favorite online retailer. I am perusing the site and adding a bunch of things to my cart for the new puppy I just got. I add puppy food that I am running low on, a new lease, a dog bowl and a water dish. I then search for tennis balls because I want my new puppy to have some toys to play with. Now am I really interested in tennis balls or dog toys? If I was at my local pet store and somebody was helping me they would clearly see that I am not really interested in tennis balls, I am actually interested in dog toys. What product embeddings bring is the ability to glean this information from my purchase experience, use vector embeddings generated for each of those products, focused on dogs, and predict what I am actually looking for, which is dog toys, not tennis balls.
Document Embeddings
Document embeddings extend the concept of text embeddings to larger bodies of text, such as entire documents or collections of documents. These embeddings capture the overall semantic meaning of a document, enabling tasks like document classification, clustering, and information retrieval. For instance, in a corporate setting, document embeddings can help categorize and retrieve relevant documents from a large internal repository based on their semantic content. They can also be used in legal tech for analyzing and comparing legal documents.
Audio Embeddings
Audio embeddings translate audio data into a vector format. This process involves extracting features from audio signals - like pitch, tone, and rhythm - and representing them in a way that can be processed by machine learning models. Applications of audio embeddings include voice recognition, music recommendation based on sound features, and even emotion detection from spoken words. Audio embeddings are crucial in developing systems like smart assistants that can understand voice commands or apps that recommend music based on a user's listening history.
Sentence Embeddings
Sentence embeddings represent individual sentences as vectors, capturing the meaning and context of the sentence. They are particularly useful in tasks such as sentiment analysis, where understanding the nuanced sentiment of a sentence is crucial. Sentence embeddings can also play a role in chatbots, enabling them to comprehend and respond to user inputs more accurately. Moreover, they are vital in machine translation services, ensuring that the translated sentences retain the original meaning and context.
Word Embeddings
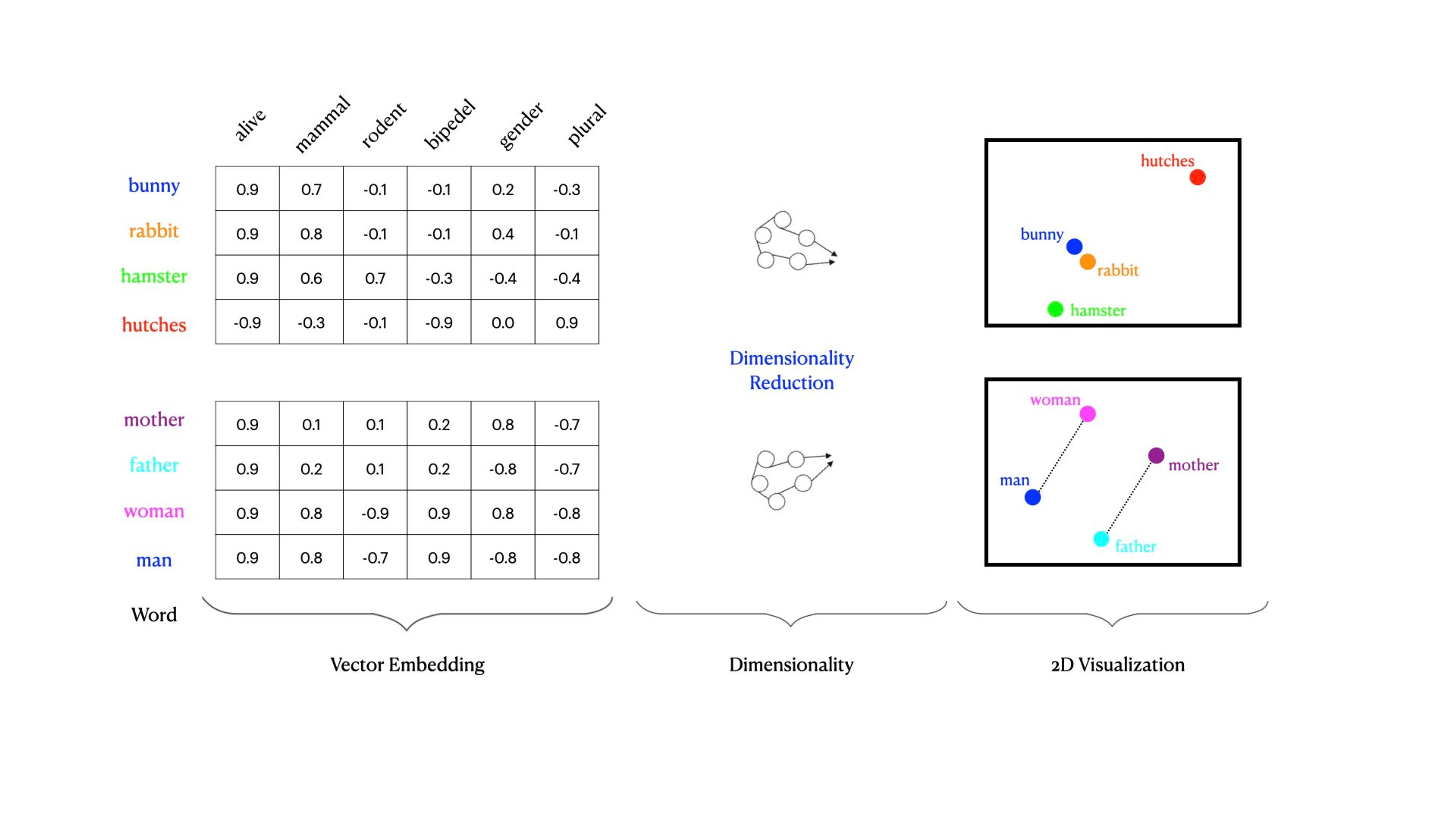
Word embeddings are the most granular form of text embeddings, where individual words are converted into vectors. These embeddings capture the semantic relationships between words, like synonyms and antonyms, and contextual usage. They are fundamental in natural language processing tasks such as text classification, language modeling, and synonym generation. Word embeddings are also used in search engines to enhance the relevance of search results by understanding the semantic meaning of the search queries.
What are the Benefits of Vector Embeddings?
Vector embeddings offer a range of benefits that make them an invaluable tool in various fields of data science and artificial intelligence:
Efficient Data Representation:
Vector embeddings provide a way to represent complex and high-dimensional data in a more manageable form. This efficient representation is crucial for processing and analyzing large datasets.
Improved Machine Learning Model Performance:
Embeddings can significantly enhance the performance of machine learning models. They allow these models to understand the nuances and relationships in the data, leading to more accurate predictions and analyses.
Semantic Understanding:
Especially in the context of text data, vector embeddings enable models to capture semantic meaning. They go beyond simple word matching, allowing the model to understand context and the relationships between words or phrases.
Facilitation of Complex Tasks:
Tasks like natural language processing, image recognition, and audio analysis become more feasible with vector embeddings. They transform raw data into a format that machine learning algorithms can efficiently work with.
Personalization and Recommendation Systems:
In e-commerce and content platforms, embeddings help in building sophisticated recommendation systems. They can identify patterns and preferences in user behavior, leading to more personalized and relevant recommendations.
Data Visualization and Clustering:
Vector embeddings can be used to visualize high-dimensional data in lower dimensions. This is valuable in exploratory data analysis, where identifying clusters and patterns is essential.
Cross-modal Data Applications:
Embeddings facilitate the interaction between different types of data, such as text and images, enabling innovative applications like cross-modal search and retrieval.
What are the Potential Challenges and Limitations of Vector Embeddings?
While vector embeddings offer numerous benefits, they also come with their own set of challenges and limitations:
Quality of Training Data:
The effectiveness of vector embeddings heavily relies on the quality of the training data. Biased or incomplete data can lead to embeddings that are skewed or inaccurate.
High-Dimensional Space Management:
Managing and processing high-dimensional vector spaces can be computationally intensive. This can pose challenges in terms of both computational resources and processing time, particularly for very large datasets.
Loss of Information:
While embeddings condense information into a more manageable format, this process can sometimes lead to the loss of subtle nuances in the data. Important details might be overlooked or underrepresented in the embedding.
Interpretability Issues:
Vector embeddings can be difficult to interpret, especially for those who are not experts in machine learning. This lack of transparency can be a hurdle in fields where understanding the decision-making process of AI models is crucial.
Generalization Versus Specificity:
Finding the right balance between making embeddings general enough to be widely applicable, yet specific enough to be useful for particular tasks, can be challenging.
Understanding these challenges is important for anyone looking to implement vector embeddings in their systems or research. It helps in making informed decisions about how best to use this technology and in anticipating potential hurdles in its application.
How to Get Started with Vector Embeddings
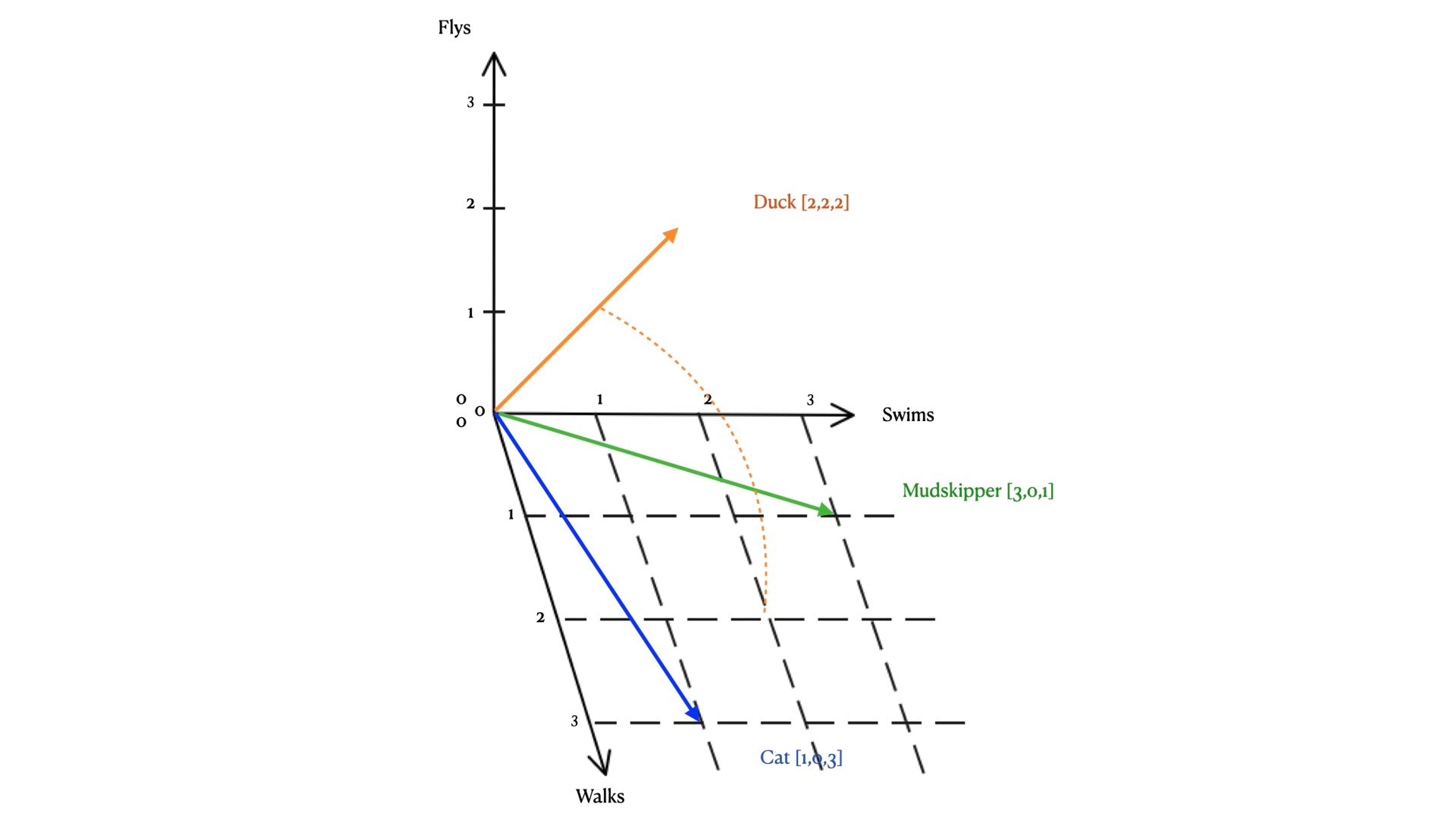
The concepts of vector embeddings can be pretty overwhelming. Anytime we try to visualize n-dimensional and use those to find semantic similarity is going to be a challenge. Thankfully there many tools available that allow for the creation of vector embeddings like Word2Vec, CNNs and many others that can take your data and turn it into vectors.
What you do with that data, how it is stored and accessed and how it is updated is where the real challenge lies.
While this may sound complex, Vector Search on Astra DB takes care of all of this for you with a fully integrated solution that provides all of the pieces you need for contextual data built for AI. From the digital nervous system, Astra Streaming, built on data pipelines that provide inline vector embeddings, all the way to real-time large volume storage, retrieval, access, and processing, via the most scalable vector database, Astra DB, on the market today, in an easy-to-use cloud platform.