Cosine Similarity Explained: A Comprehensive Guide

What is Cosine Similarity?

Cosine similarity is a mathematical metric used to measure the similarity between two vectors in a multi-dimensional space, particularly in high-dimensional spaces, by calculating the cosine of the angle between them.

This is our comprehensive guide on cosine similarity, an essential concept in the field of data science, text analysis, machine learning, and much more. If you've ever wondered what cosine similarity is or how it's used in real-world applications, you're in the right place.

Cosine similarity is a mathematical way to measure how similar two sets of information are. In the simplest terms, it helps us understand the relationship between two elements by looking at the "direction" they are pointing in, rather than just comparing them based on their individual values.

Imagine you're a book lover, and you've rated three books: "The Lunar Mystery," "Secrets of the Ocean," and "Flight of the Phoenix." You've rated them on a scale of 1 to 5. Your friend has also rated these same books on the same scale:

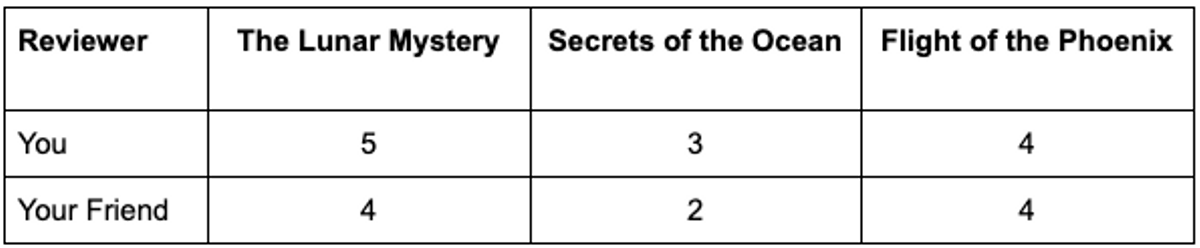
Both of your ratings can be represented as lists or, in mathematical terms, as "vectors", represented as [5,3,4] and [4,2,4].

Do you and your friend have similar ratings? You can look at the lists and come up with a qualitative “yes they’re pretty close”, or you can use cosine similarity to reach a quantitative measure! We will come back to this example, but cosine similarity is a concept that has far-reaching applications in areas like search engines, natural language processing, and recommendation systems.

Cosine similarity provides a means of understanding how data relates to each other, without getting bogged down by the specific details of what each data point represents. It also allows us to quickly compare information with tens, hundreds, or even thousands of elements.

Significance of Cosine Similarity

Cosine similarity is widely used in applications like natural language processing (NLP), search algorithms, and recommendation systems. It provides a robust way to understand the semantic similarity between documents, datasets, or images. For example, cosine similarity is often used in vector search engines to find the most relevant records to a given query, making search processes more efficient and precise. (For more information on vector search, you may reference this explainer!)

Purpose and Scope of this Guide

This guide aims to give you an in-depth understanding of what cosine similarity is, its mathematical underpinnings, its advantages, and its varied applications in different domains. The guide will also share some Python code to complement your understanding.

By the end of this guide, you'll be well-equipped to understand, implement, and make the most of cosine similarity in your projects or research.

Cosine similarity explained

Understanding the concept of cosine similarity is crucial for various applications, from data analysis to Natural Language Processing (NLP). But what is cosine similarity exactly? How is it used, and how does it differ from other similarity metrics? In this section, we'll dig deeper into these questions.

Definition of Cosine Similarity

Cosine similarity is a metric that measures the cosine of the angle between two non-zero vectors in a multi-dimensional space. Mathematically, it is computed as the dot product of the vectors divided by the product of their magnitudes (lengths). We’ll get into the exact meaning of that later, but for now simply understand that the closer the value is to 1, the more similar the vectors are. Cosine similarity is effective because it captures the orientation (or "direction") of the vectors and not their magnitude, making it sensitive to the similarities in the pattern of the data, and insensitive to the magnitude of the vectors.

An Example of Cosine Similarity

Let's revisit our book ratings example for a moment. We had two vectors:

Your ratings: [5,3,4]

Your friend's ratings: [4,2,4]

Using cosine similarity, we can quantify how similar these vectors are. The cosine similarity will return a value between -1 and 1; a value closer to 1 indicates greater similarity. In our example, calculating the cosine similarity gives us a value 0.9899, suggesting that you and your friend have very similar tastes in books. If you had another friend with ratings of [1,5,2], the cosine similarity would be 0.7230, suggesting less similar tastes.

The site math3d.org can provide a helpful way to visualize two and three-dimensional vectors. With our simple example vectors, we can see that the angle between [5,3,4] and [4,2,4] is smaller than the angle between [5,3,4] and [1,5,2]:

Source: https://www.math3d.org/7tCJuIQal

If you are wondering “If smaller angles mean two vectors are more similar, why are we not just using the angles - why all this complicated math?”, we will be answering that later on!

Importance in Data Analysis and NLP

Cosine similarity is invaluable in fields like data analysis and natural language processing. In NLP, it is frequently used for tasks such as text mining, sentiment analysis, and document clustering. The metric helps in comparing two pieces of text to understand their semantic similarity, which is crucial for making accurate recommendations or categorizations.

A real-world example of a customer making use of cosine similarity is Dataworkz. They are a California-based company that aims to simplify AI-driven decision-making for business users through its no-code, cloud-based platform. The service unifies data gathering, transformation, and the application of machine learning algorithms into a single user-friendly interface. You can read more about what they are doing here.

How Cosine Similarity Differs from Other Similarity Metrics

There are various ways to measure similarity between sets of data, with Euclidean distance being another commonly used metric. While Euclidean distance focuses on the straight-line distance between two points in space, cosine similarity focuses on the angle between two vectors. This makes cosine similarity more robust in capturing the pattern similarities between two sets of data, even if their magnitudes differ.

For example, if two documents have the same words but in different frequencies, Euclidean distance might consider them quite different due to the differences in magnitude (frequency). Cosine similarity, however, would capture their similarity more effectively because it is less sensitive to the frequency of the words and more focused on their presence or absence in the documents.

A “close cousin” to cosine similarity is dot product similarity. It is typically used when the vectors are already normalized (their magnitudes are 1), thereby avoiding the computational step of dividing by the product of their magnitudes (which will always be 1!). A number of vector embedding models output normalized vectors, making dot product similarity calculations faster.

Put Cosine Similarity into Practice with Vector Search on AstraDB

To sum up, cosine similarity offers a robust, effective way to measure similarity that has broad applications, especially in NLP and data analysis. Its focus on the orientation rather than the magnitude of the vectors sets it apart from other similarity metrics like Euclidean distance. Whether you are analyzing text data, making recommendations, or engaging in complex data analysis, understanding the nuances of cosine similarity can be immensely beneficial.

Ready to put cosine similarity into practice? Vector Search on AstraDB is a comprehensive solution that helps you analyze and understand complex data. Learn more here!

Advantages of cosine similarity

Cosine similarity is a widely-used metric that has several advantages in various applications, such as text analysis, recommendation systems, and more. Below are some key benefits that make it a go-to choice for measuring similarity between vectors.

Scale-invariant

Cosine similarity is scale-invariant, meaning that it is not affected by the magnitudes of the vectors. This is especially useful in scenarios where you want to focus solely on the directionality of the vectors, rather than their length. Whether the values in your vector are in the tens or the millions, the cosine similarity will remain the same, making it versatile across different scales.

Dimensionality Reduction

Another advantage of using cosine similarity is its compatibility with techniques like Principal Component Analysis (PCA) and t-distributed Stochastic Neighbor Embedding (t-SNE). Because it measures similarity in terms of angle rather than distance, you can reduce the dimensions of your vectors without significantly affecting the cosine similarity measure.

Simplicity and Efficiency

The formula for calculating cosine similarity is straightforward, requiring just the dot product of the vectors and their magnitudes. This simplicity leads to efficient computations, making it suitable for real-time applications and large datasets.

Angle Measurement

Unlike other distance-based similarity measures, cosine similarity considers the angle between vectors, providing a more intuitive sense of similarity. Smaller angles indicate higher similarity, and the measure ranges between -1 and 1, making interpretation easier.

Widely Used in Text Analysis

Cosine similarity is particularly popular in the field of text analysis. When documents are converted into embedding vectors, cosine similarity effectively captures the "angle" between different documents, highlighting how closely the contents are related.

By considering these advantages, it becomes clear why cosine similarity is a popular choice in various machine learning and data science applications.

Unraveling the Power of Cosine Similarity

As we wrap up, let's take a moment to summarize what we've discussed in this extensive guide on cosine similarity. We delved deep into the core principles of this fascinating metric, showing you its mathematical foundations. And don't forget about its numerous advantages, including its scale-invariant nature and its compatibility with dimensionality reduction techniques, which make it an essential tool in the fields of machine learning and data science.

Now, if you're interested in putting your newfound knowledge into practical use, DataStax's Astra DB offers an excellent platform for executing vector searches with built-in cosine similarity calculations. Astra DB's Vector Search feature handles the heavy lifting, allowing you to focus more on deriving insights from your data.

The Vector Search Overview documentation contains a number of quick-starts and tutorials that can help you build real-world applications that leverage cosine similarity search, including not only chatbots but also image searching!

To start your journey with Astra DB, you can register for a free account here.