Exploring the Real-world Applications of Cosine Similarity
In information retrieval systems like search engines, cosine similarity measures the relevance of documents to a query. How does this enhance the effectiveness of search results?

Real-World Applications of Cosine Similarity
Cosine similarity is not just a theoretical concept; it has a wide range of practical applications in various domains. From simplifying searches in large datasets to understanding natural language, and from personalizing user experiences to classifying documents, cosine similarity is an indispensable tool. Below, we delve into some key areas where this metric is often applied.
But first, we should remind ourselves “What are we comparing?” We are using “embedding vectors” to represent real-world information. An embedding is a vector representation of some data that preserves the meaning of the data. Embeddings can be created by machine learning models, but they can also be created by software designed to capture meaningful data. We don’t even need software to capture embeddings - taking real-world measurements of something like the dimensions of a flower can be represented as vector embeddings.
Information Retrieval
Cosine similarity is frequently used in information retrieval systems, such as search engines. When you enter a search query, the engine uses cosine similarity to measure the relevance of documents in its database to the query. This ensures that the most similar and relevant documents are returned, enhancing the efficiency and effectiveness of the search. Text information is commonly embedded with simple algorithms like Bag-of-Words, or more complex trained models that are built with neural networks such as Word2Vec, GloVe, and Doc2Vec. Large Language Models (LLMs) such as GPT, BERT, LLaMa, and their derivatives are increasingly used in this space.
Text Mining and Natural Language Processing (NLP)
In text mining and NLP, cosine similarity is used to understand the semantic relationships between different pieces of text. Whether it's summarizing documents, comparing articles, or even determining the sentiment of customer reviews, this metric helps in understanding the context and content similarity among different textual data points. Different text embedding techniques like TF-IDF, Word2Vec, or BERT can be used to transform raw text into vectors that can then be compared using cosine similarity. LLMs are also widely deployed in NLP applications, particularly in the realm of autonomous agents and chatbots.
Recommendation Systems
Personalization is key in today's digital experiences, and cosine similarity is a crucial component of recommendation systems that drive personalization. For example, Netflix uses cosine similarity to suggest movies based on your watching history. The system represents each movie and user as vectors and then utilizes cosine similarity to find the movies that are closest to your preferences and past viewing patterns. Embeddings are generated using techniques like Matrix Factorization or AutoEncoders.
Image Processing
In image processing, cosine similarity can be used to measure the likeness between different images or shapes. Vector embeddings for images are typically generated using Convolutional Neural Networks (ConvNets or CNNs) or other deep learning techniques to capture the visual patterns in the images. This is particularly useful in facial recognition systems, in identifying patterns or anomalies in medical imaging, and in self-driving vehicles, among other applications.
Document Classification
Document classification is another application where cosine similarity is invaluable. Documents can be embedded using techniques like TF-IDF or Latent Semantic Indexing (LSI, also known as Latent Semantic Analysis), and these vectors can be compared to predefined category vectors to automate document classification processes. Search engines make extensive use of this, including not only internet search engines but also domain-specific search engines such as those found in fields of law and forensics.
Clustering and Data Analysis
Cluster analysis is a method for grouping similar items and is often a precursor step. It's not tied to a single algorithm but employs various approaches and techniques. Cosine similarity is a popular metric used in these algorithms, thus aiding in efficiently finding clusters in high-dimensional data spaces. Fine-tuning of the vectors is achieved by adjusting the embedding model output until a suitable data structure is revealed. The tuned embedding model can then be used as part of a real-world application.
By understanding and leveraging cosine similarity in these various domains, one can optimize processes, enhance user experiences, and make more informed decisions.
The mathematics behind cosine similarity
“Complicated Math”
Previously we asked the question “Why all this complicated math?” While it might seem intuitive to simply use the angle between two vectors to measure their similarity, there are several advantages to using the cosine similarity formula:
- First, calculating the actual angle would require trigonometric operations like arccosine, which are computationally more expensive than the dot and magnitude operations in the cosine formula.
- Second, cosine similarity yields a value between -1 and 1, making it easier to interpret and compare across multiple pairs of vectors.
- Lastly, cosine similarity inherently normalizes the vectors by their magnitudes. This means it accounts for the 'length' of the vectors, ensuring that the similarity measure is scale-invariant.
So, while the angle or the Euclidean distance between the two vectors could give us some sense of similarity, the cosine similarity formula offers a more efficient and easy-to-interpret metric.
Understanding Vector Representation
In cosine similarity, the primary prerequisite is the representation of data as vectors. A vector is essentially an ordered list of numbers that signify magnitude and direction. In the context of cosine similarity, vectors serve as compact, mathematical representations of the data. For example, a document can be represented as a vector where each component of the vector corresponds to the frequency of a particular word in the document. This kind of vector representation is fundamental to the cosine similarity calculation.
The Cosine Formula and Its Intuitive Interpretation
The cosine formula used in cosine similarity offers an intuitive way to understand the relationship between two vectors. Mathematically, the cosine similarity formula is expressed as:
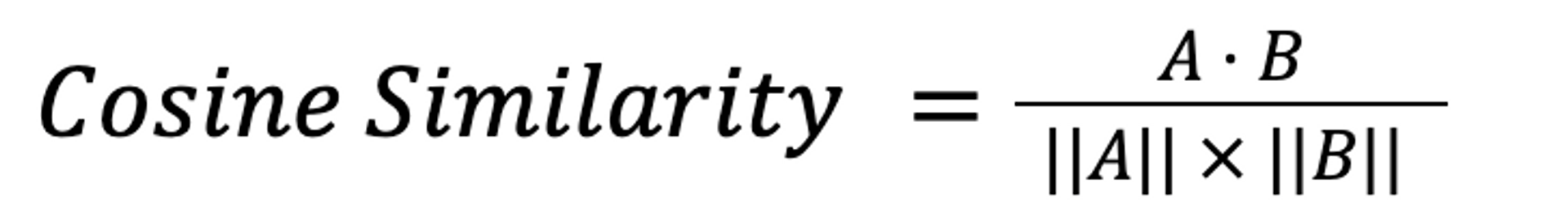
where AB is the dot product of the vectors A and B, while AB is the product of the magnitudes of the vectors A and B. This is the traditional, most compact representation of Cosine Similarity but to those without some training in linear algebra, it can be hard to understand. We will use a mathematically equivalent formula to show a way to calculate this easily.
The result of this equation is the cosine of the angle between the two vectors. An angle of 0 degrees results in a cosine similarity of 1, indicating maximum similarity. The angle between the vectors offers an intuitive sense of similarity: The smaller the angle, the more similar the vectors are. The greater the angle, the less similar they are.

Steps for Calculating Cosine Similarity
An alternate formulation uses more familiar sums, squares, and square roots:
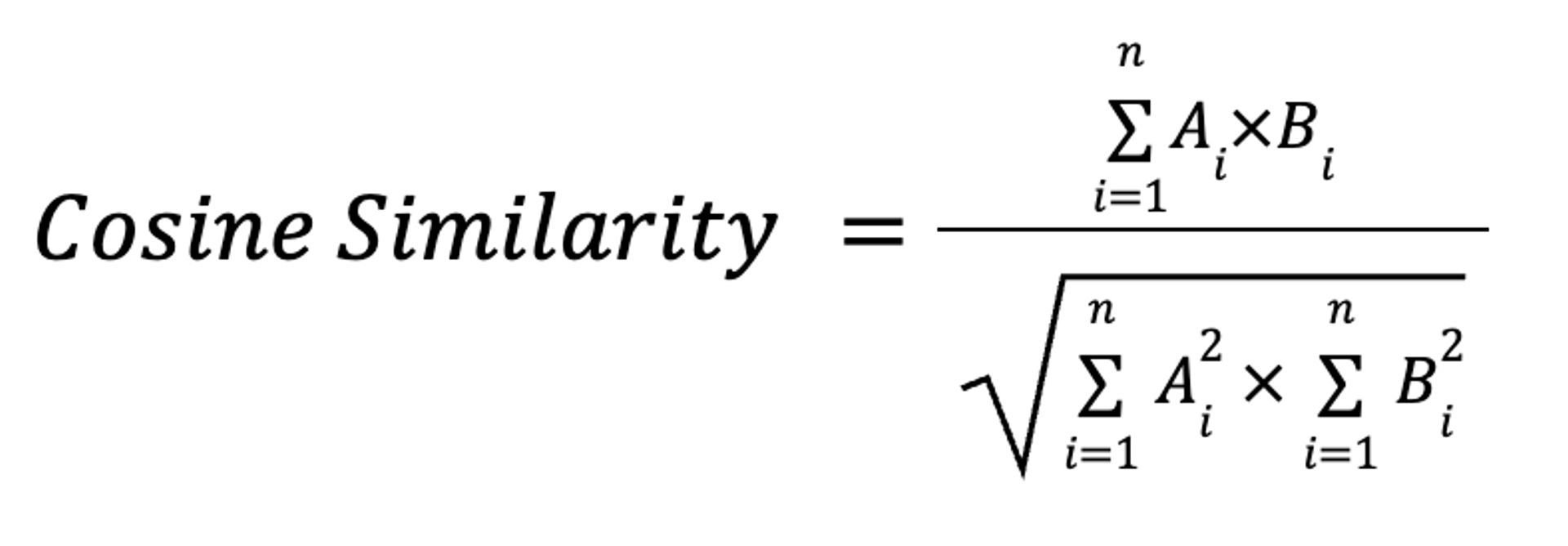
where Ai and Bi are the ith components of vectors A and B. This is how we will explain the mathematics of cosine similarity.
First is the numerator, or the dot product. To calculate this, multiply the corresponding components in each vector. For an n-dimensional vector, this would be:
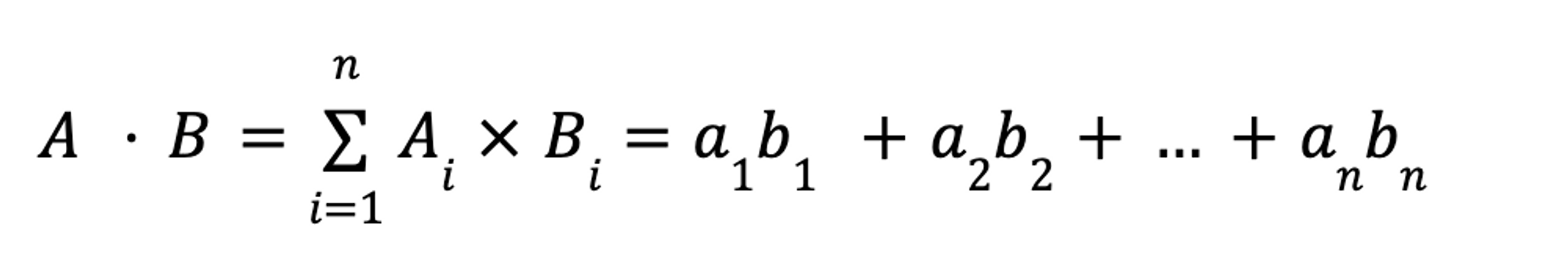
For example, our two book review vectors [5,3,4] and [4,2,4] would compute as:
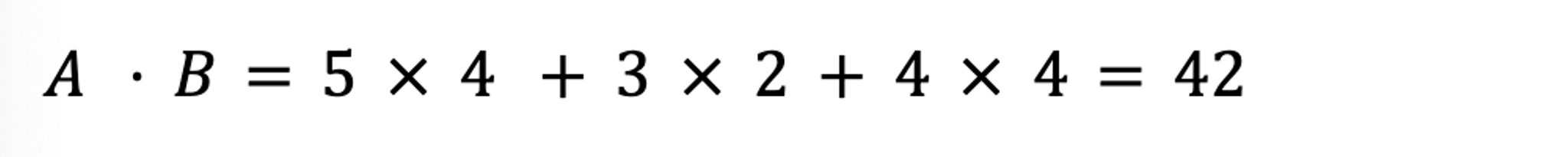
Second, the denominator, or the product of the magnitudes. Here, we compute each vector independently, and then multiply the two components:
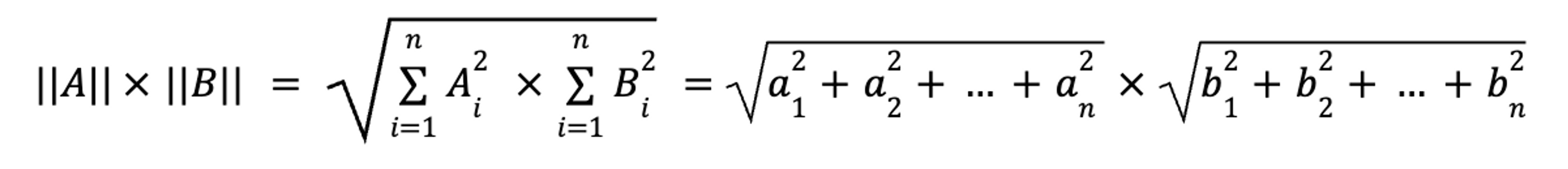
For our book review vectors:
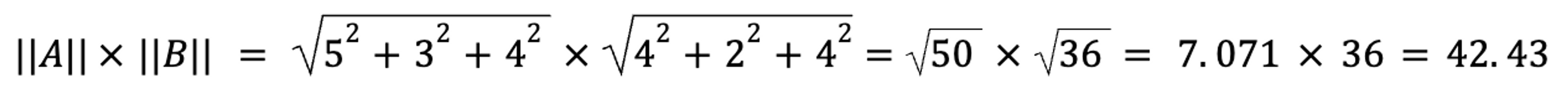
Finally, divide the second value into the first value:

And for our book review vectors:

Which means that you and your friend have reviewed the three books similarly.
In case you didn’t realize it, you’ve just done a linear algebra calculation. If it is your first, congratulations! By following these steps, you can accurately and intuitively measure the similarity between two sets of data, regardless of their size.
The “Dot Product” Cousin
Earlier, it was mentioned that there is a similarity calculation called “dot product similarity”, and that it was a close cousin to cosine similarity. Consider what would happen if all the vectors were normalized - their magnitudes would all have a value of 1. In this case, to compute the cosine similarity we could forgo the product of the magnitudes calculation - if the magnitude of each vector is 1, then 11 =1. This is the reason that many embeddings return normalized vectors - it reduces the amount of calculations that need to be performed.
Use Cosine Similarity with Vector Search on Astra DB
Ready to put cosine similarity into practice? Vector Search on Astra DB is now available - and it does the math for you! Understand your data, derive insights, and build smarter applications today. You can register now and get going in minutes!


